A binary Heap is a tree structure it is compact as possible, all the children of the node are as full as they can and the left children are filled first.
Type of Binary Heap
Max Binary Heap
Min Binary Heap
Max Binay Heap its parent node is always larger than its child node at every level down the tree.
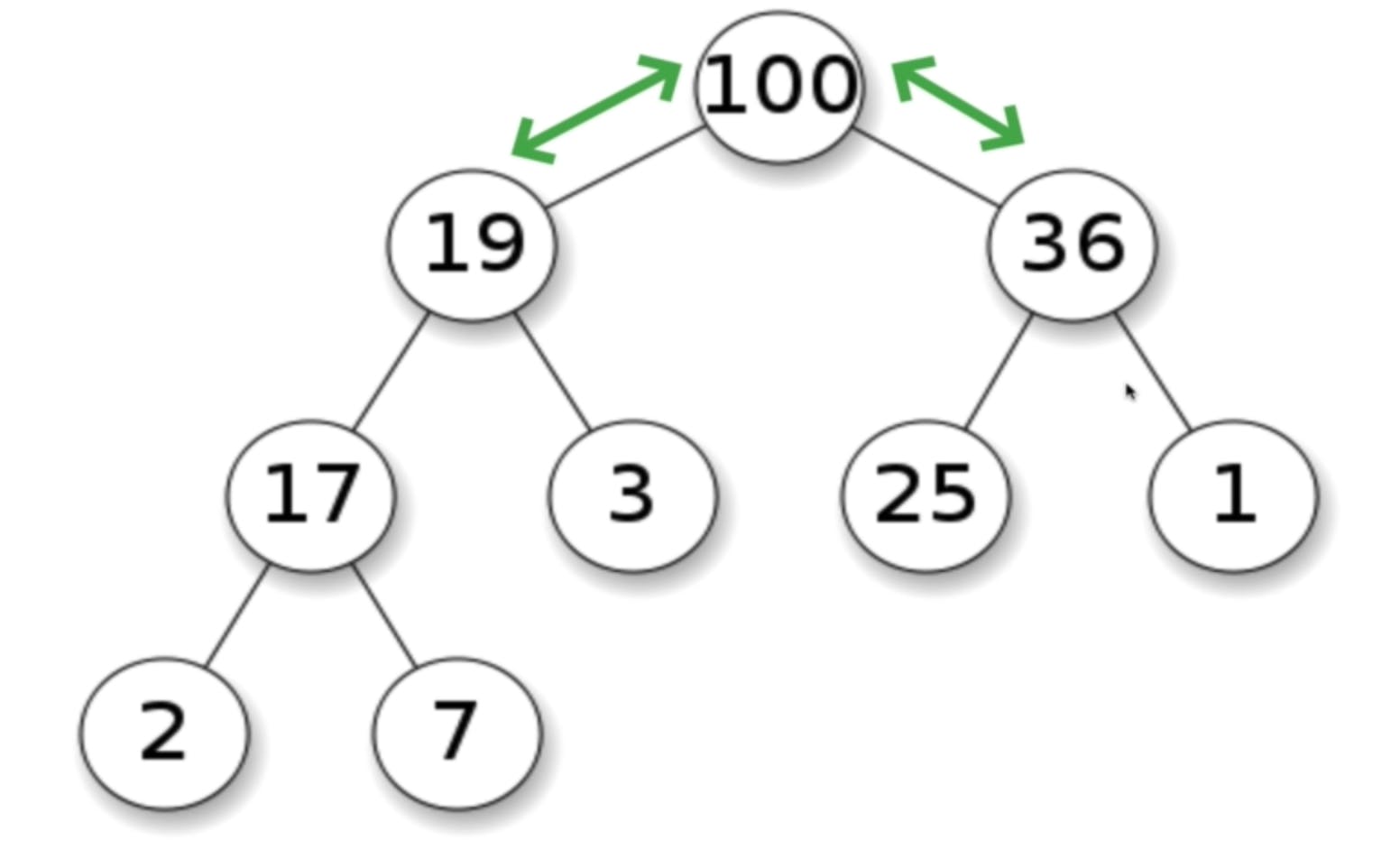
Min Binary Heap its parent node is always smaller than its child node at every level down the tree.

Why heap
Binary heaps are used to implement priority queues and it's a very common data structure they are also used with graph traversal algorithms.
Storing Heap
lis and array are commonly used to store heap which is a built in data structure for any programming language.
Storing heap as a List

Storing Heap as an array

therefore, for any index "n" inside of an array, the left child node is stored at (2n+1) while its right child node is stored at (2n+2).

For example below array when its parent is at index "3" we found its left child by multiplying 3 by 2 and then adding 1 to it which gives "7" (2n +1) and then we found its right child by multiplying the parent index by 2 and then add 2 to which gives "8" (3*2+2) 2n +2

Insert to a Max Binary Heap.
The process of inserting something to a Binary heap is to fill out from left to an array, which basically pushes to the array and we then do something to the new value of the array which is called bubbling up what that means is to swap it until we find its correct resting place in the array, in max Binary Heap the large value is going to bubble up to the correct spot and then do a comparison.

Pushing "55" to an array, by putting it there its index means it is a child of "33" with this (n-1)/2 reversing the previous operation and "33" is index of "2" and its children are index "5" and "6" so next bubble up which is to compare "55" to its parent then swap because "55" is larger.


class MaxBinaryHeap {
constructor() {
this.val = []
}
insert(element) {
this.val.push(element)
this.bubbleUp()
}
bubbleUp() {
let index = this.val.length - 1
const element = this.val[index]
while (index > 0) {
let parentIdx = Math.floor((index - 1) / 2)
let parent = this.val[parentIdx]
if (element <= parent) break
if(element > parent){
this.val[parentIdx] = element
this.val[index] = parent
}
index = parentIdx
}
}
}
// [41,39,33,18,27,12,55]
// 0 1 2 3 4 5 6
Big O of Binary heap
For insertion, the time complexity is O(logn) which is basically O(log base 2 to n)
each time we go down a step in binary structure we have 2 times the number of nodes
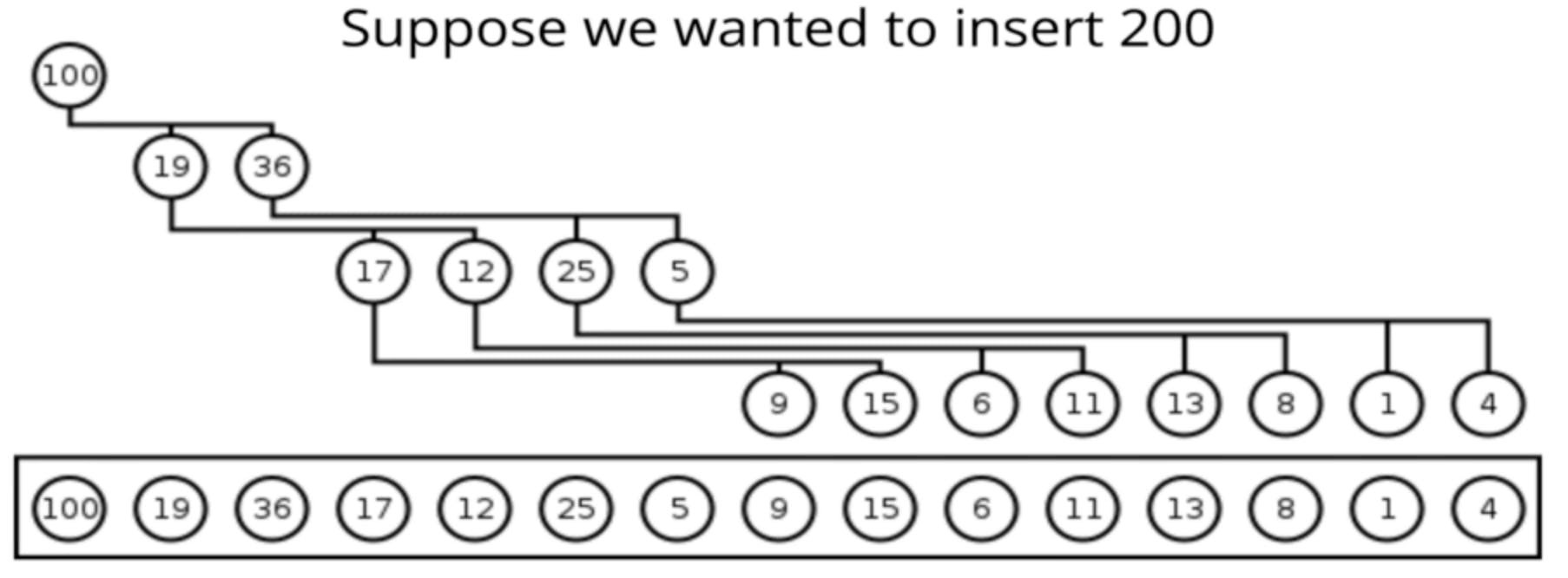
Suppose we wanted to insert '200' to this Binary heap, this is worst case because it is the largest number and it is going to end up at the starting point of this Binary queue. We only have to compare it one time per step therefore for 16 elements there are 4 comparisons which is 2 to what power gives 16 === 4 (2*2*2*2) however It's the same Idea for removal O(logn) as well.

